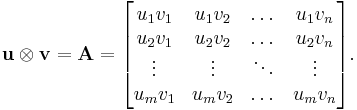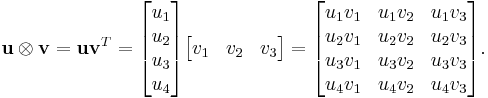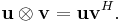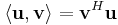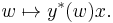Outer product

For "outer product" in geometric algebra, see exterior product.

In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix. The name contrasts with the inner product, which takes as input a pair of vectors and produces a scalar.

The outer product of vectors can be also regarded as a special case of the Kronecker product of matrices.

Some authors use the expression "outer product of tensors" as a synonym of "tensor product". The outer product is also a higher-order function in some computer programming languages such as APL and Mathematica.

Contents

Definition

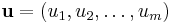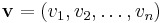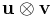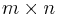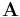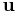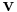Given a vector \mathbf{u}=(u_1, u_2, \dots, u_m) with m elements and a vector \mathbf{v}= (v_1, v_2, \dots, v_n) with n elements, their outer product \mathbf{u} \otimes \mathbf{v} is defined as the m\times n matrix \mathbf{A} obtained by multiplying each element of \mathbf{u} by each element of \mathbf{v}:

\mathbf{u} \otimes \mathbf{v} = \mathbf{A} = \begin{bmatrix}u_1v_1 & u_1v_2 & \dots & u_1v_n \\ u_2v_1 & u_2v_2 & \dots & u_2v_n \\ \vdots & \vdots & \ddots & \vdots\\ u_mv_1 & u_mv_2 & \dots & u_mv_n \end{bmatrix}.

Note that 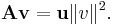\mathbf{A} \mathbf{v} = \mathbf{u} \Vert v \Vert ^2.

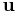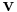For complex vectors, it is customary to use the complex conjugate of \mathbf{v} (denoted \bar{\mathbf{v}}). Namely, matrix \mathbf{A} is obtained by multiplying each element of \mathbf{u} by the complex conjugate of each element of \mathbf{v}.

Definition (matrix multiplication)

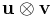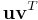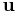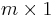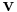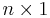The outer product \mathbf{u} \otimes \mathbf{v} as defined above is equivalent to a matrix multiplication \mathbf{u} \mathbf{v}^T, provided that \mathbf{u} is represented as a m\times 1 column vector and \mathbf{v} as a n \times 1 column vector (which makes 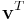\mathbf{v}^T a row vector). For instance, if 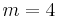m = 4 \, and n = 3, \,

\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^T = \begin{bmatrix}u_1 \\ u_2 \\ u_3 \\ u_4\end{bmatrix} \begin{bmatrix}v_1 & v_2 & v_3\end{bmatrix} = \begin{bmatrix}u_1v_1 & u_1v_2 & u_1v_3 \\ u_2v_1 & u_2v_2 & u_2v_3 \\ u_3v_1 & u_3v_2 & u_3v_3 \\ u_4v_1 & u_4v_2 & u_4v_3\end{bmatrix}.

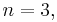
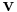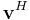For complex vectors, it is customary to use the conjugate transpose of \mathbf{v} (denoted \mathbf{v}^H):

\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^H.

Contrast with inner product

If m = n, then one can take the matrix product the other way, yielding a scalar (or 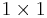1 \times 1 matrix):

\left\langle \mathbf{u}, \mathbf{v}\right\rangle = \mathbf{v}^H \mathbf{u}

which is the standard inner product for Euclidean vector spaces, better known as the dot product. The inner product is the trace of the outer product.

Definition (abstract)

Let V and W be two vector spaces, and let W* be the dual space of W. Given a vector x ∈ V and y* ∈ W*, then the tensor product y* ⊗ x corresponds to the map A : W → V given by

w \mapsto y^*(w)x.

Here y*(w) denotes the value of the linear functional y* (which is an element of the dual space of W) when evaluated at the element w ∈ W. This scalar in turn is multiplied by x to give as the final result an element of the space V.

Thus intrinsically, the outer product is defined for a vector and a covector; to define the outer product of two vectors requires converting one vector to a covector (in coordinates, transpose), which one can do in the presence of a bilinear form 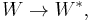W \to W^*, generally taken to be a nondegenerate form (meaning this is an isomorphism) or more narrowly an inner product.

If V and W are finite-dimensional, then the space of all linear transformations from W to V, denoted Hom(W,V), is generated by such outer products; in fact, the rank of a matrix is the minimal number of such outer products needed to express it as a sum (this is the tensor rank of a matrix). In this case Hom(W,V) is isomorphic to W* ⊗ V.

Contrast with inner product

For more details on this topic, see Inner product space#Other products.

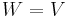If W=V, then one can also pair the covector w*∈V* with the vector v∈V via 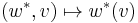(w^*,v)\mapsto w^*(v), which is the duality pairing between V and its dual, sometimes called the inner product.

Definition (tensor multiplication)

The outer product on tensors is typically referred to as the tensor product. Given a tensor a with rank q and dimensions (i 1, ..., i q), and a tensor b with rank r and dimensions (j 1, ..., j r), their outer product c has rank q+r and dimensions (k 1, ..., k q+r) which are the i  dimensions followed by the j  dimensions. For example, if A has rank 3 and dimensions (3, 5, 7) and B has rank 2 and dimensions (10, 100), their outer product c has rank 5 and dimensions (3, 5, 7, 10, 100). If A[2, 2, 4] = 11 and B[8, 88]= 13 then C[2, 2, 4, 8, 88] = 143. .

To understand the matrix definition of outer product in terms of the definition of tensor product:

  1. The vector v can be interpreted as a rank 1 tensor with dimension (M), and the vector u as a rank 1 tensor with dimension (N). The result is a rank 2 tensor with dimension (M, N).
  2. The rank of the result of an inner product between two tensors of rank q and r is the greater of q+r-2 and 0. Thus, the inner product of two matrices has the same rank as the outer product (or tensor product) of two vectors.
  3. It is possible to add arbitrarily many leading or trailing 1 dimensions to a tensor without fundamentally altering its structure. These 1 dimensions would alter the character of operations on these tensors, so any resulting equivalences should be expressed explicitly.
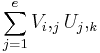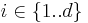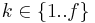  4. The inner product of two matrices V with dimensions (d, e) and U with dimensions (e, f) is \sum_{j = 1}^e V_i,_j U_j,_k where i \in \{1..d\} and k \in \{1..f\}, For the case where e =1, the summation is trivial (involving only a single term).

The term "rank" is used here in its tensor sense, and should not be interpreted as matrix rank.

Applications

The outer product is useful in computing physical quantities (e.g., the tensor of inertia), and performing transform operations in digital signal processing and digital image processing. It is also useful in statistical analysis for computing the covariance and auto-covariance matrices for two random variables.

See also

Products

Duality

Topics related to linear algebra